Capítulo 8 \(IMA(d,q)\): Proceso Integrado y de Media Móvil
Este proceso es un caso particular del proceso \(ARIMA(p,d,q)\) cuando \(p=0\). Se calculan las diferencias de la serie de tiempo \(d\) veces para convertir la serie en estacionaria y luego se aplica un modelo \(MA(q)\).
Por ejemplo:
Sea \(Z_1, Z_2, Z_3, Z_4, Z_5\) la serie de tiempo original. Entonces la serie diferenciada de orden uno será:
\[ \begin{array}{c} Y_1=Z_2-Z_1\\ Y_2=Z_3-Z_2\\ Y_3=Z_4-Z_3\\ Y_4=Z_5-Z_4 \end{array} \]
Y la serie diferenciada de orden dos será:
\[ \begin{split} X_1=Y_2+Y_1=Z_3-Z_2+Z_2-Z_1=Z_3-Z_1\\ X_2=Y_3+Y_2=Z_4-Z_2\\ X_3=Y_4+Y_3=Z_5-Z_3 \end{split} \] Por lo tanto al hacer diferencia de orden 2 a la serie de tiempo original \(Z_t\), se obtiene una serie de tiempo \(X_1, X_2, X_3\) que ya es estacionaria y a esta se la aplicaría un modelo de medias móviles \(MA(q)\), por ejemplo si \(q=1\) se ajustaría un modelo \(X_t=X_{t-1}+\epsilon_t\), donde \(\epsilon_t\) es ruido blanco.
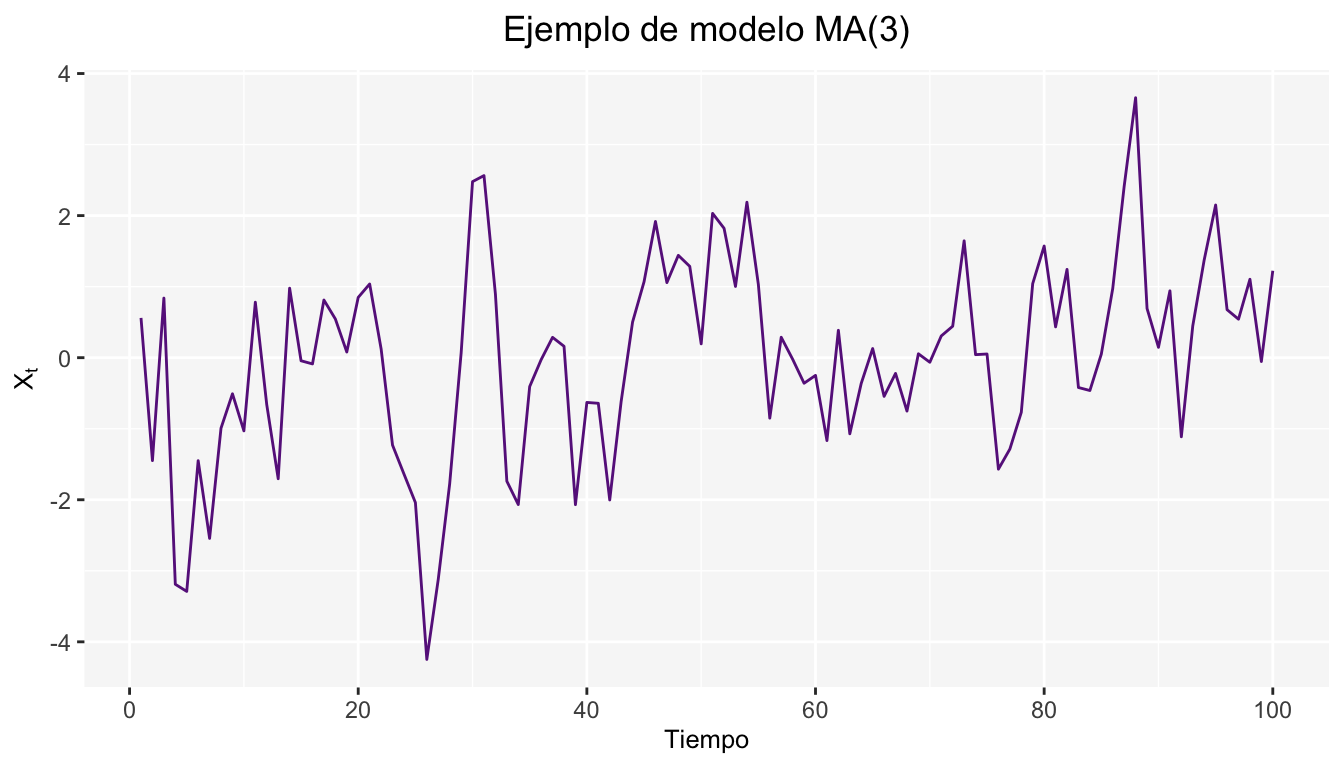
A continuación se modelan los datos de un modelo \(MA(3)\) de la siguiente forma \(X_t=0.80\epsilon_{t-1}+0.20\epsilon_{t-2}+0.50\epsilon_{t-3}\)
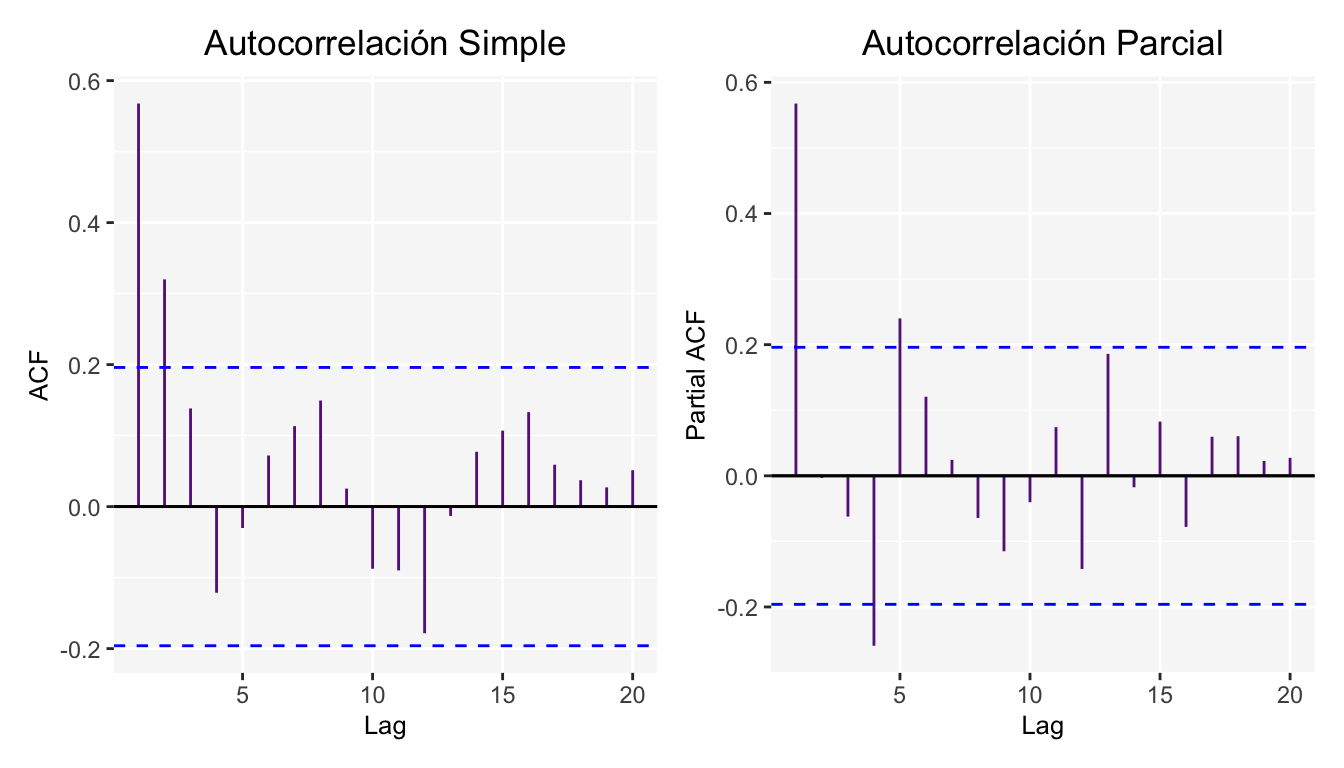
Además de las gráficas de Autocorrelación simple y parcial.
Ahora veamos como queda la serie si le incluimos un proceso integrado (una diferencia) de orden 1.
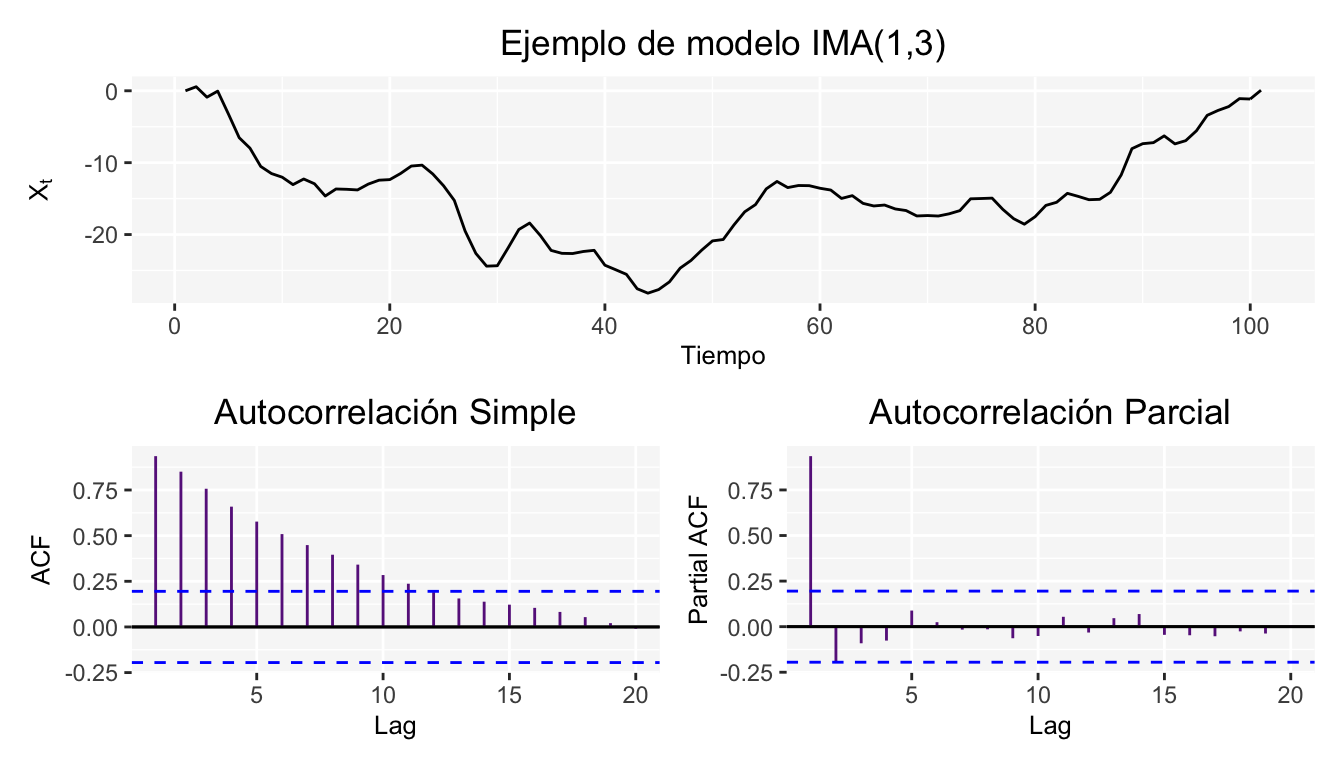
Haga la prueba aumentando el orden de las diferencias, ¿cuál es el efecto en la serie de tiempo?