Capítulo 13 $GARCH(p,q)$: Proceso Autoregresivo Generalizado con Heterocedasticidad Condicional

En el modelo $ARCH(1)$ el predictor al tiempo $t + 1$ de la varianza depende solo del último valor de $\sigma_t$. Sin embrago, en la práctica se desea tener mayor precisión en la predicción, para mejorarla se podría incluir todos los valores pasados $\sigma_t$ con menor peso para volatilidades más distantes. Una propuesta para este problema la desarrolló Bollerslev(1986), donde introduce $p$ retrasos de la varianza condicional al modelo, entonces $p$ hace referencia al orden del modelo GARCH.

Entonces un proceso estacionario $X_t$ sigue un modelo $GARCH(p,q)$ si $$X_t=\sigma_t\epsilon_t$$ donde $\epsilon_t$ es ruido blanco y $$\sigma^2_{t} = \alpha_0+\sum_{i=1}^q \alpha_i X^2_{t-i}+\sum_{j=1}^p \beta_j\sigma^2_{t-j}$$ Donde $\alpha_0>0$,$\alpha_i\ge0, i=1,...,q$ y $\beta_j\ge0, j=1,...,p$. Para garantizar que la varianza sea positiva y existan los momentos de orden superior se requiere que $\sum_{i=1}^{max(p,q)}(\alpha_i+\beta_i)<1$.

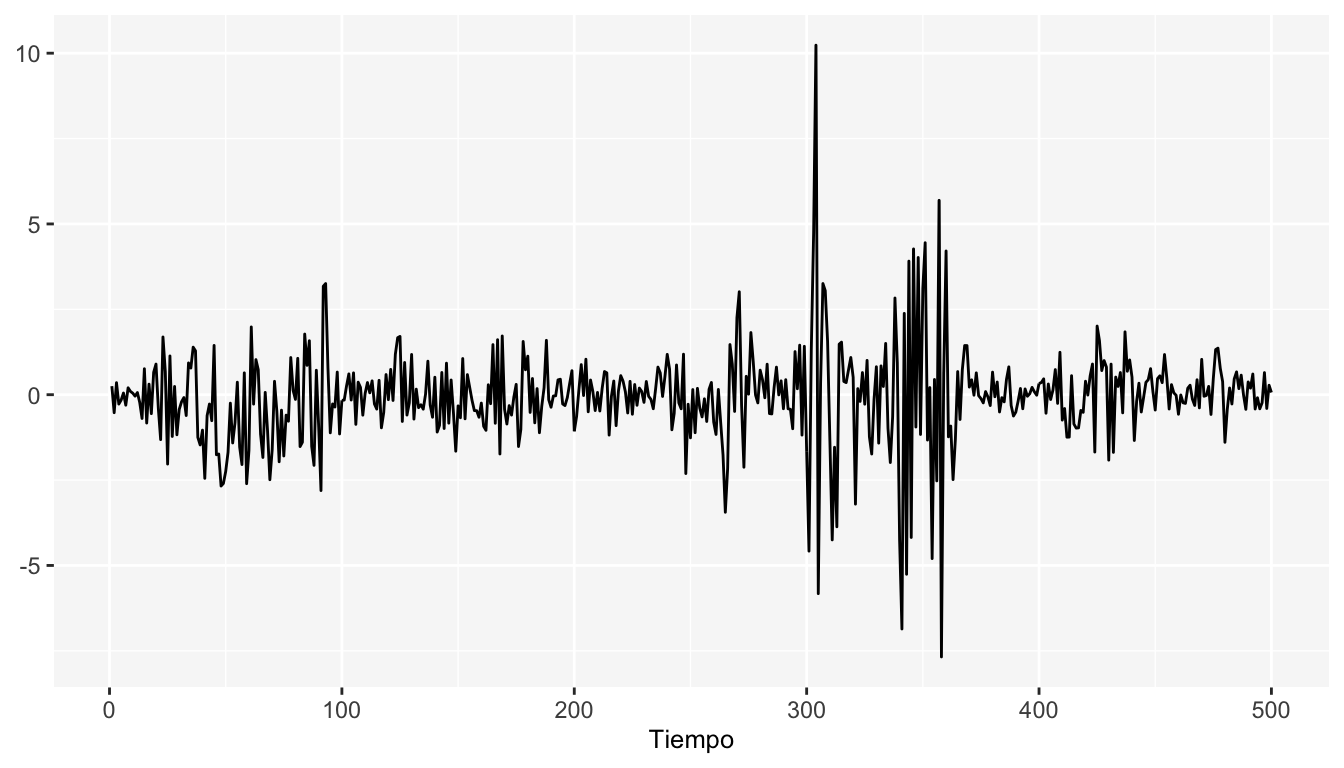
A continuación se muestran las simulaciones de un modelo $GARCH(1,1)$ con la varianza modelada de la siguiente forma: $\sigma^2_{t}=0.05+ 0.4X_{t-1}+0.55\sigma^2_{t-1}$

Cryer, Jonathan D, and Kung-Sik Chan. 2008. Time Series Analysis: With Applications in R. Springer Science & Business Media.

Holmes, E, and EJ Ward. 2019. Applied Time Series Analysis for Fisheries and Environmental Sciences. University of Washington, Lecture Material.

Hyndman, Rob J, and George Athanasopoulos. 2018. Forecasting: Principles and Practice. OTexts.

Nielsen, Aileen. 2019. Practical Time Series Analysis: Prediction with Statistics and Machine Learning. " O’Reilly Media, Inc.".

William, WS, and S Wei. 2006. Time Series Analysis: Univariate and Multivariate Methods. Second. Pearson/Addison-Wesley Reading.