Capítulo 7 \(ARIMA(p,d,q)\): Proceso Autoregresivo Integrado y de Medias Móviles
Los modelos de series de tiempo \(AR\), \(MA\) y \(ARMA\) se basan en el supuesto de estacionariedad del proceso, es decir, la media, la varianza y las covarianzas son constantes en el tiempo. Sin embrago, muchas series de tiempo relacionadas con aplicaciones reales no son estacionarias, ya sea porque cambian de nivel en el tiempo (existe tendencia) o la varianza no es constante en el tiempo, a este tipo de procesos se les conoce como procesos integrados.
Para trabajar con estas series de tiempo lo que se hace es calcular las diferencias de la serie de tiempo \(d\) veces para hacerla estacionaria y posteriormente aplicar a la serie diferenciada un modelo \(ARMA(p,q)\), en este caso se diría que la serie original es un proceso \(ARIMA(p,d,q)\), donde \(p\) es el número de términos autoregresivos, \(d\) el número de veces que la serie debe ser diferenciada para hacerla estacionaria y \(q\) el número de términos de la media móvil.
La expresión algebraica del proceso \(ARIMA(p,d,q)\) es:
\[ X_t^d=c+\phi_1X_{t-1}^d+...+\phi_pX_{t-p}^d-\theta_1\epsilon_{t-1}^d-\theta_2\epsilon_{t-2}^d-...-\theta_q\epsilon_{t-q}^d+\epsilon_t^d \]
donde \(X_t^d\) es la serie de las diferencias de orden \(d\), \(\epsilon_t^d\) es un proceso de ruido blanco, y \(\phi_1,...,\phi_p,\theta_1,...,\theta_q\) son los parámetros del modelo.
El modelo \(ARIMA(p,d,q)\) se puede escribir en términos de los operadores de retardo de la siguiente manera:
\[ \begin{array}{c} (1-\phi_1B-\phi_2B^2-...-\phi_pB^p)X_t^d=c+(1-\theta_1B-\theta_2B^2-...-\theta_qB^q)\epsilon_t^d\\ \phi_p(B)(1-B)^dX_t=c+\theta_q(B)\epsilon_t^d \end{array} \] Los modelos integrados se usan para reducir la NO estacionariedad de la serie al usar las diferencias y en la mayoría de las aplicaciones \(d=1\) y hasta \(d=2\) es suficiente para volver la serie estacionaria, pero en algunas ocasiones, aplicar transformaciones a los datos tienen mejor resultado para lograr la estacionariedad en comparación con las diferencias. Por ejemplo, en las series de tiempo económicas, la variabilidad aumenta cuando el nivel promedio del proceso aumenta. Sin embargo el porcentaje de cambio en las observaciones es relativamente independiente del nivel, entonces aplicar una transformación logarítmica puede ser más eficiente para lograr la estacionariedad de la serie.
Ejemplo
Se tiene el siguiente modelo: \(X_t = \mu_t +Z_t\) donde \(\mu_t = \beta_0+\beta_1t\) y \(Z_t\) es un proceso estacionario.
\[ \begin{split} X_t -X_{t-1} &= \mu_t+Z_t-\mu_{t-1}-Z_{t-1}\\ & = \beta_0+\beta_1t+Z_t-\beta_0-\beta_1(t-1)-Z_{t-1}\\ & = \beta_1+Z_t-Z_{t-1} \end{split} \]
El cual ya no depende de \(t\).
A continuación se muestran los resultados para un modelo \(ARIMA(2,1,1)\) de la siguiente forma \(X_t=0.85X_{t-1}-0.45X_{t-2}+.30\epsilon_{t-1}\)
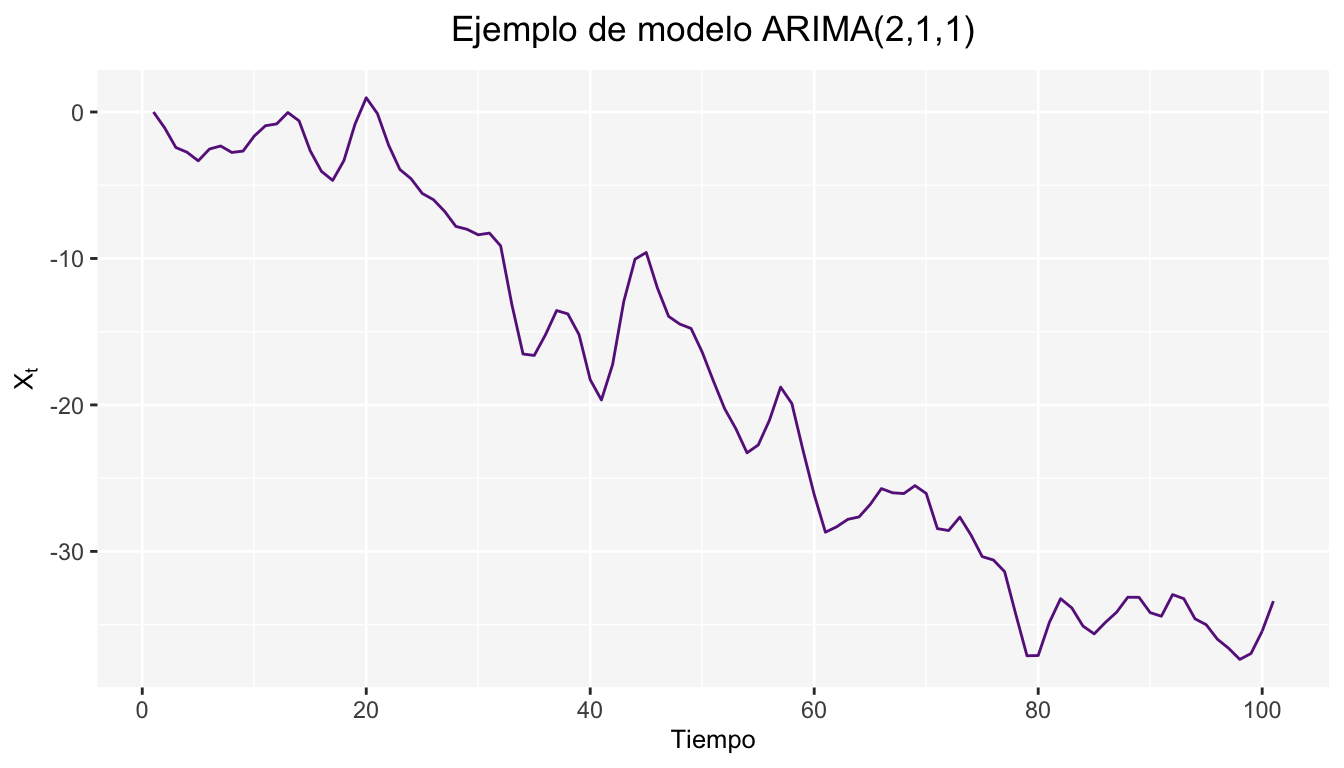
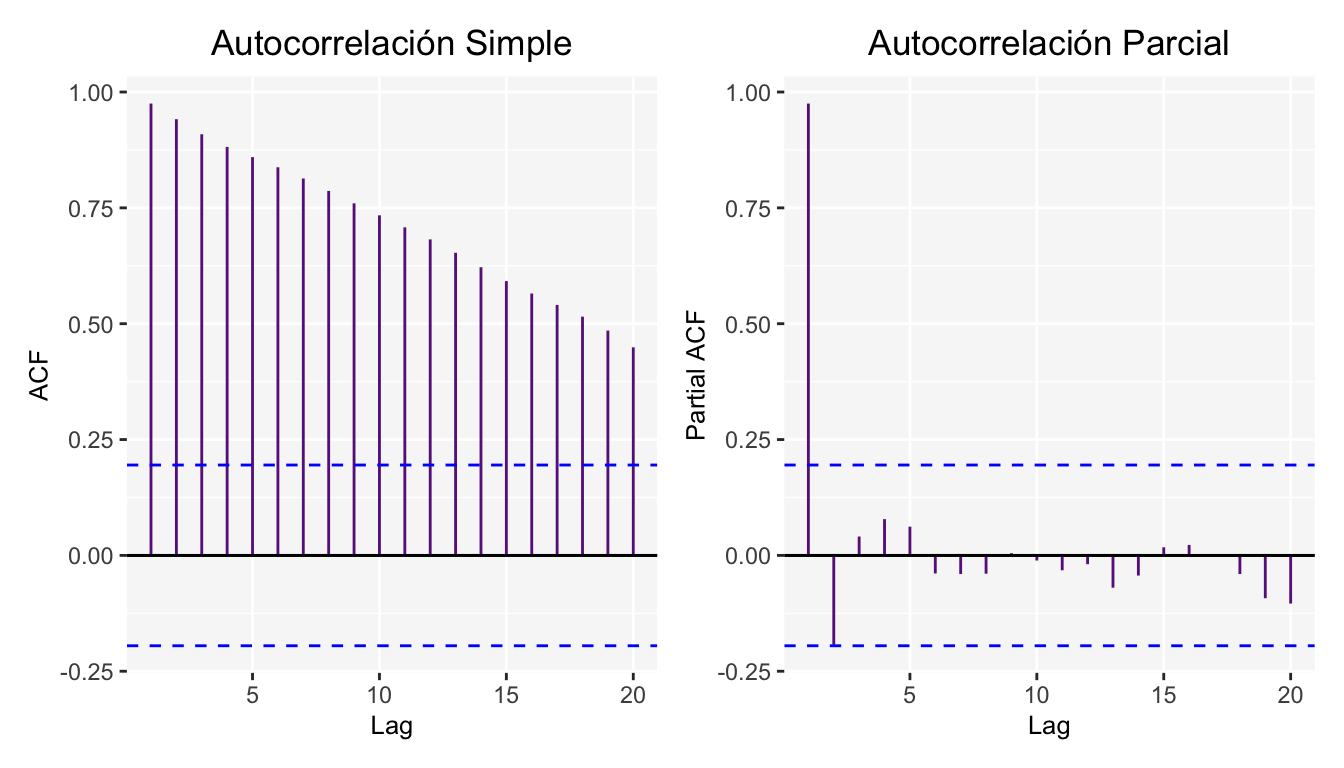
Además de las gráficas de Autocorrelación simple y parcial.
A continuación se muestran los resultados para un modelo \(ARIMA(2,2,1)\) de la siguiente forma \(X_t=0.85X_{t-1}-0.45X_{t-2}+.30\epsilon_{t-1}\)
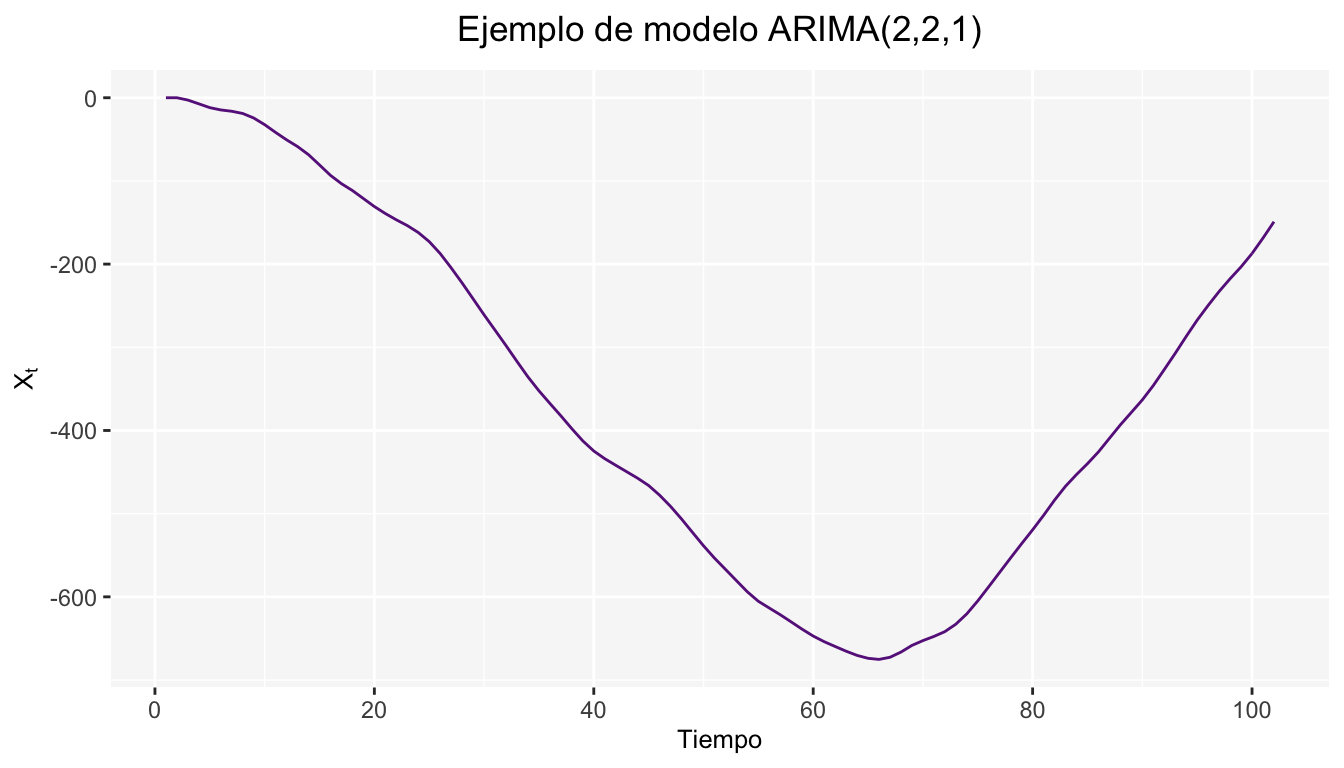
Además de las gráficas de Autocorrelación simple y parcial.
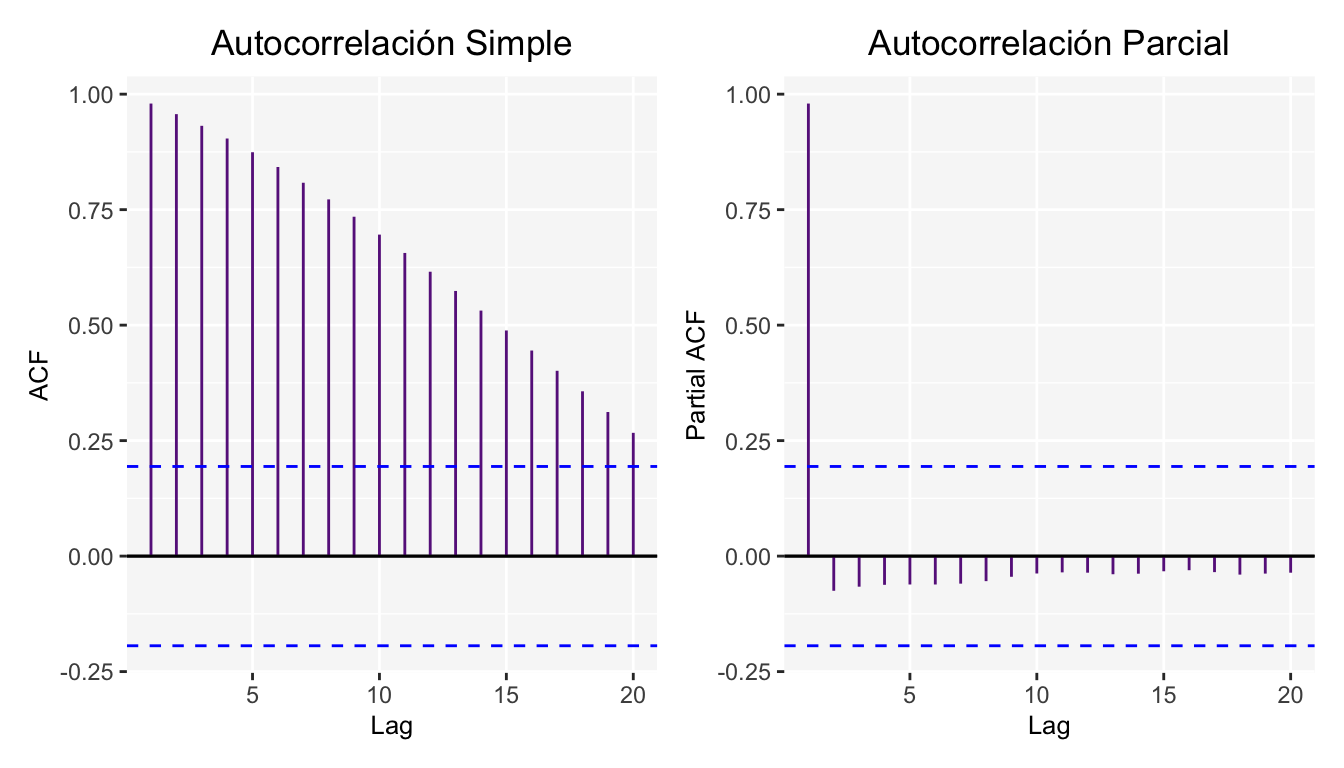
¿Qué se puede decir del efecto que tiene el parámetro \(d\) al comparar las gráficas de ambas series?