Capítulo 5 Modelos Paramétricos
Existen varios modelos paramétricos que se emplean en el análisis de supervivencia, esto se debe a que pueden representar de manera adecuada el comportamiento de ciertos fenómenos. La motivación para usar un modelo en particular es, por lo general, empírica; o bien, con base en la información que proporcione algún modelo No paramétrico. Las familias paramétricas más importantes son: Exponencial, Weibull, Log-Normal, Log-logística y Gamma.
5.1 Modelo Exponencial
El modelo exponencial es el más importante debido a su amplia aplicación, por ejemplo, puede emplearse en estudios para determinar el tiempo de vida útil de algunos artículos manufacturados. Este modelo juega un papel fundamental análogo a la distribución normal en la inferencia estadística tradicional.
Función de Densidad
\[ f(t)=h(t)S(t)=\lambda exp(-\lambda t)=\lambda e^{-\lambda t} \] Para esta distribución \(\lambda\) es un parámetro que modifica la escala de la distribución. Este es comúnmente llamado tasa definido por \(1/s\) donde \(s\) es el verdadero parámetro de escala4 de la distribución. Es muy común utilizar este parámetro en lugar del parámetro de escala ya que simplifica la expresión matemática.
Función de Supervivencia
\[ S(t)=exp\left(-\int_0^{t}h(u)du\right)=exp\left(-\int_0^{t}\lambda du\right)=exp(-\lambda t)=e^{-\lambda t} \]
Si asumimos una tasa de riesgo invariante en el tiempo, \(h(t)=\lambda\) con \(\lambda>0\), generamos el modelo exponencial:
Función de Riesgo
Tomamos \(\lambda>0\) y hacemos:
\[ h(t)=\lambda \]
Aunque el supuesto de una función de riesgo constante resulta ser una restricción considerable, el modelo exponencial no deja de ser útil e importante en variedad de aplicaciones. Cabe destacar, que este modelo cumple con la propiedad de pérdida de memoria; a saber, se cumple que:
\[ \mathbb{P}(T>t+x|T>t)=\mathbb{P}(T>x) \]
Parámetros
Si \(T\sim Exp(\lambda)\) entonces:
\[ \mathbb{E}[T]=\int_{0}^{\infty}t\lambda e^{-\lambda t}dt=\frac{1}{\lambda} \]
Y
\[ Var[T]=\mathbb{E}[T^2]-\mathbb{E}[T]^2=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}=\frac{1}{\lambda^2} \]
Gráficas
A continuación se muestran gráficas de una \(Exponencial\) con \(\lambda=0.5\)

R
En el lenguaje de programación R se pueden obtener resultados de esta distribución como una muestra pseudo aleatoria y aproximaciones numéricas para la distribución y densidad de esta así como la obtención de los cuantiles.
En general, el sufijo para esta distribución es *exp, de tal manera que se tienen las siguientes funciones mencionando la interpretación de sus resultados:
rexp(n, rate = 1): Muestra pseudo aleatoria de tamaño \(n\).dexp(x, rate = 1, log = FALSE): Valores de \(f(x)\).pexp(q, rate = 1, lower.tail = TRUE, log.p = FALSE): Valores de \(F(x)\).qexp(p, rate = 1, lower.tail = TRUE, log.p = FALSE): Cuantil \(t_p\).
Algo que hay que recordar es que al utilizar la función, por ejemplo, rexp(n, r) se respeta el orden de los parámetros por lo que r será el valor correspondiente a la tasa y no parámetro de escala es decir el valor \(r = \lambda\). Se menciona esta por que puede ser común que se confunda r con \(1/\lambda\), por lo que se recomienda tener precaución.
5.2 Modelo Weibull
El modelo Weibull es una generalización del modelo exponencial, se agrega un parámetro de forma5 \(\gamma\) y se mantiene el parámetro de escala \(\lambda\). Este modelo es uno de los más utilizados para tiempos de falla: tiene utilidad en la vida de algunos artículos manufacturados, así como en los tiempos de aparición de tumores en medicina.
Función de Densidad \[ f(t)=\lambda \gamma(\lambda t)^{\gamma-1}e^{-(\lambda t)^\gamma}=h(t)S(t) \]
Obsérvese que si \(\gamma =1\) entonces el modelo Weibull se reduce al modelo exponencial.
Función de Supervivencia
\[ S(t)=exp\left(-\int_0^{t}h(u)du\right)=exp\left(-\int_0^{t}\lambda \gamma(\lambda u)^{\gamma-1} du\right)=exp(-(\lambda t)^\gamma)=e^{-(\lambda t)^\gamma} \]
Si asumimos, en general, una función de riesgo monótona: creciente o decreciente, se puede obtener el modelo Weibull.
Función de Riesgo
Para este modelo \(h(t)\) está dada por:
\[ h(t)=\lambda \gamma(\lambda t)^{\gamma-1}; \ \ \ \gamma>0, \lambda>0 \mbox{ y } t>0 \]
Parámetros
Si \(T\sim Weibull(\gamma,\lambda)\) entonces:
\[ \mathbb{E}[T]=\frac{1}{\lambda}\Gamma\left(\frac{1}{\gamma}+1\right) \]
Y además
\[ Var[T]=\frac{1}{\lambda^2}\Gamma\left(\frac{2}{\gamma}+1\right)-\left(\frac{1}{\lambda}\Gamma\left(\frac{1}{\gamma}+1\right)\right)^2 \\=\frac{1}{\lambda^2}\left[\Gamma\left(\frac{2}{\gamma}+1\right)-\left(\Gamma\left(\frac{1}{\gamma}+1\right)\right)^2\right] \] Debe resultar sencillo para el alumno demostrar las igualdades de la esperanza y varianza.
Gráficas
Las dos gráficas siguientes muestran curvas de \(f(t)\) y \(h(t)\) para el modelo Weibull con \(\lambda=1\) y \(\gamma=2,4\):
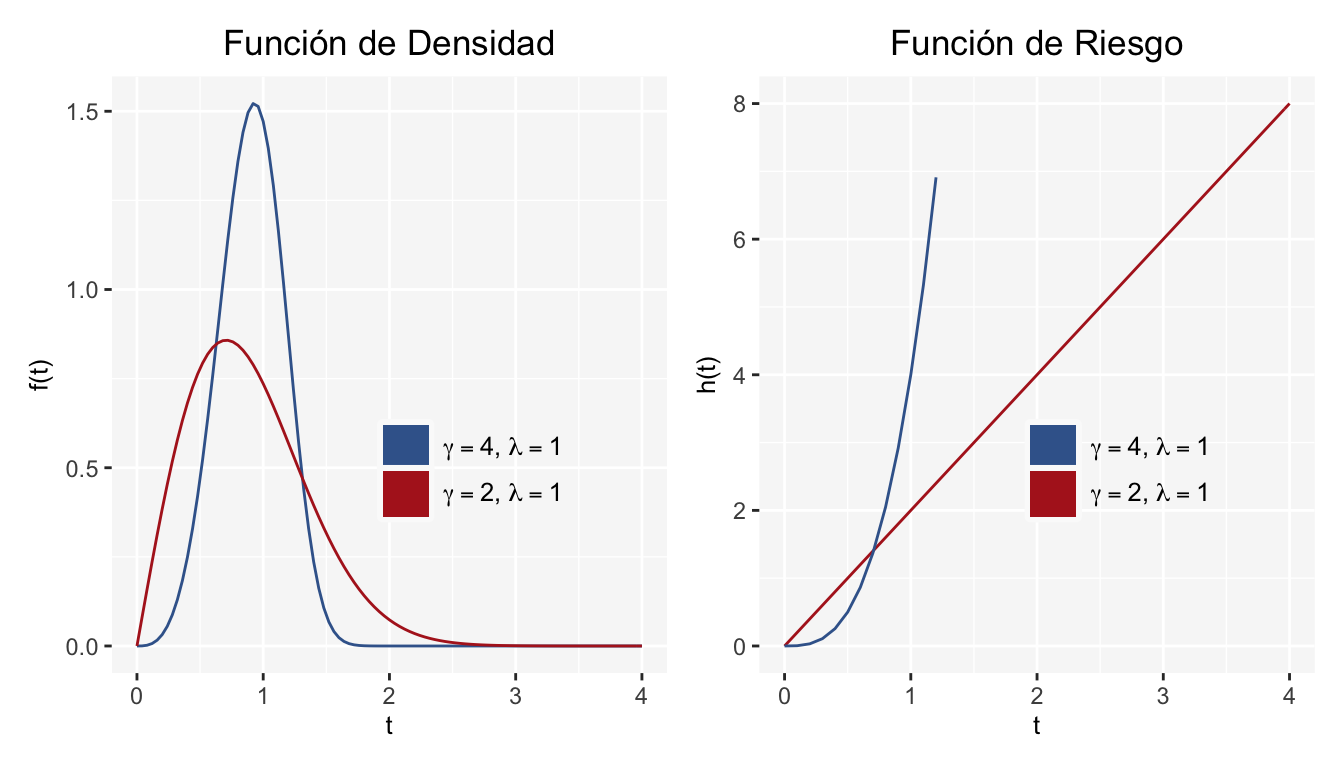
Y para el modelo Weibull con \(\lambda=1\) y \(\gamma=0.5,1\) se tienen las siguientes gráficas:
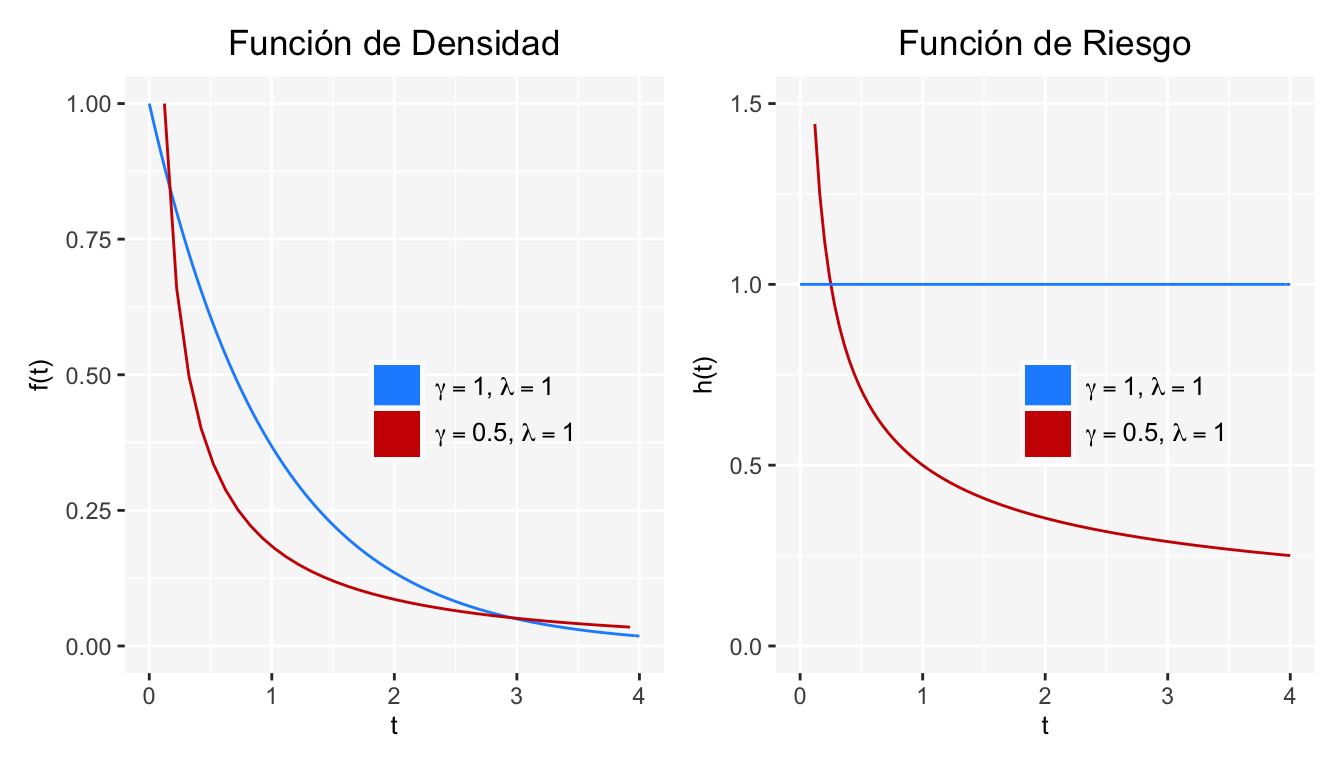
Como bien hemos dicho, si suponemos una función de riesgo monótona creciente ó decreciente la distribución Weibull puede ser generada. Concretamente, si \(\gamma>1\) entonces \(h(t)\) es estrictamente creciente, si \(\gamma<1\) entonces \(h(t)\) es estrictamente decreciente. Cuando \(\gamma=1\) se tiene la distribución exponencial.
R
Para este caso el sufijo referente a esta distribución es *weibull, de tal manera que se tienen las siguientes funciones mencionando la interpretación de sus resultados:
rweibull(n, shape, scale = 1): Muestra pseudo aleatoria de tamaño \(n\).dweibull(x, shape, scale = 1, log = FALSE): Valores de \(f(x)\).pweibull(q, shape, scale = 1, lower.tail = TRUE, log.p = FALSE): Valores de \(F(x)\).qweibull(p, shape, scale = 1, lower.tail = TRUE, log.p = FALSE): Cuantil \(t_p\).
Así como en el caso de la exponencial y en todos los casos posteriores, se respeta el orden de los parámetros por lo que para aplicar los parámetros tal como se vieron en esta sección se puede utilizar esta función de la siguiente manera: dweibull(\(\gamma\), \(1/\lambda\)) o sin importar el orden indicando de manera explicita que shape = \(\gamma\) y scale = \(1/\lambda\). Esto último debido a que la función de densidad para este modelo en R esta considerada como \(f(x) = \frac{\gamma}{\lambda}(\frac{x}{\lambda})^{\gamma-1}e^{-(\frac{x}{\lambda})^\gamma}\).
5.3 Modelo Log-Normal
El modelo Log-Normal tiene estrecha relación con la distribución Normal. De hecho, el tiempo de supervivencia \(T\) se dice que sigue una distribución Log-Normal, si \(Y=ln(T)\) se distribuye \(N(\mu,\sigma^2)\).
La distribución Log-Normal se ha utilizado como modelo en el tiempo de falla de aislantes eléctricos y en el tiempo de aparición de cáncer pulmonar. También se utiliza en poblaciones que son una mezcla de tiempos de vida cortos y largos. A pesar de esto, este modelo es criticado por ser decreciente para valores grandes de \(t\), lo cual parece inadecaudo en algunas situaciones.
Función de Densidad
Para este modelo, \(f(t)\) está dada por:
\[ f(t)=\frac{1}{\sqrt {2\pi}\sigma t}exp\left(-\frac{1}{2}\left(\frac{ln(t)-\mu}{\sigma}\right)^2\right) \]
En este caso, \(\mu\) y \(\sigma\) pasan a ser los parámetros de escala y de forma de la distribución, los cuales hacen diferencia con los de la distribución normal, ya que en tal caso \(\mu\) sería un parámetro de localización y \(\sigma\) seguiría siendo el parámetro de escala. Para agregar un parámetro de localización a la distribución \(log-normal\) bastaría camiar \(x\) por \(x-\theta\) donde \(\theta\) sería tal parámetro.
Función de Supervivencia
\[ S(t)=\int_t^{\infty}f(u)du \\=1-\int_0^{t}f(u)du \\=1-\int_0^{t}\frac{1}{\sqrt {2\pi}\sigma u}exp\left(-\frac{1}{2}\left(\frac{ln(u)-\mu}{\sigma}\right)^2\right)du \]
Tomando la notación de la función de distribución de una Normal estándar, \(\Phi()\), se tiene:
\[ S(t)=1-\Phi\left(\frac{ln(t)-\mu}{\sigma}\right) \]
Función de Riesgo
\[ h(t)=\frac{f(t)}{S(t)} \\=\frac{\frac{1}{\sqrt {2\pi}\sigma t}exp\left(-\frac{1}{2}\left(\frac{ln(t)-\mu}{\sigma}\right)^2\right)}{1-\Phi\left(\frac{ln(t)-\mu}{\sigma}\right)} \]
Si bien la expresión de \(h(t)\) parece ser complicada, su gráfica resulta ser más interesante. Ésta toma el valor de cero en \(t=0\), crece hasta un valor máximo y luego tiende a cero cuando \(t \rightarrow \infty\). Véase sección de gráficas.
Parámetros
Si \(T\sim LogNormal(\mu,\sigma^2)\) entonces:
\[ \mathbb{E}[T]=exp\left(\mu+\frac{\sigma^2}{2}\right) \]
Y además
\[ Var[T]=exp(2\mu+2\sigma^2)-exp(2\mu+\sigma^2) \]
La demostración de las igualdades de media y varianza se dejan al alumno.
Gráficas
A continuación algunos ejemplos de las gráficas de \(f(t)\) y \(h(t)\) para la distribución Log-Normal:
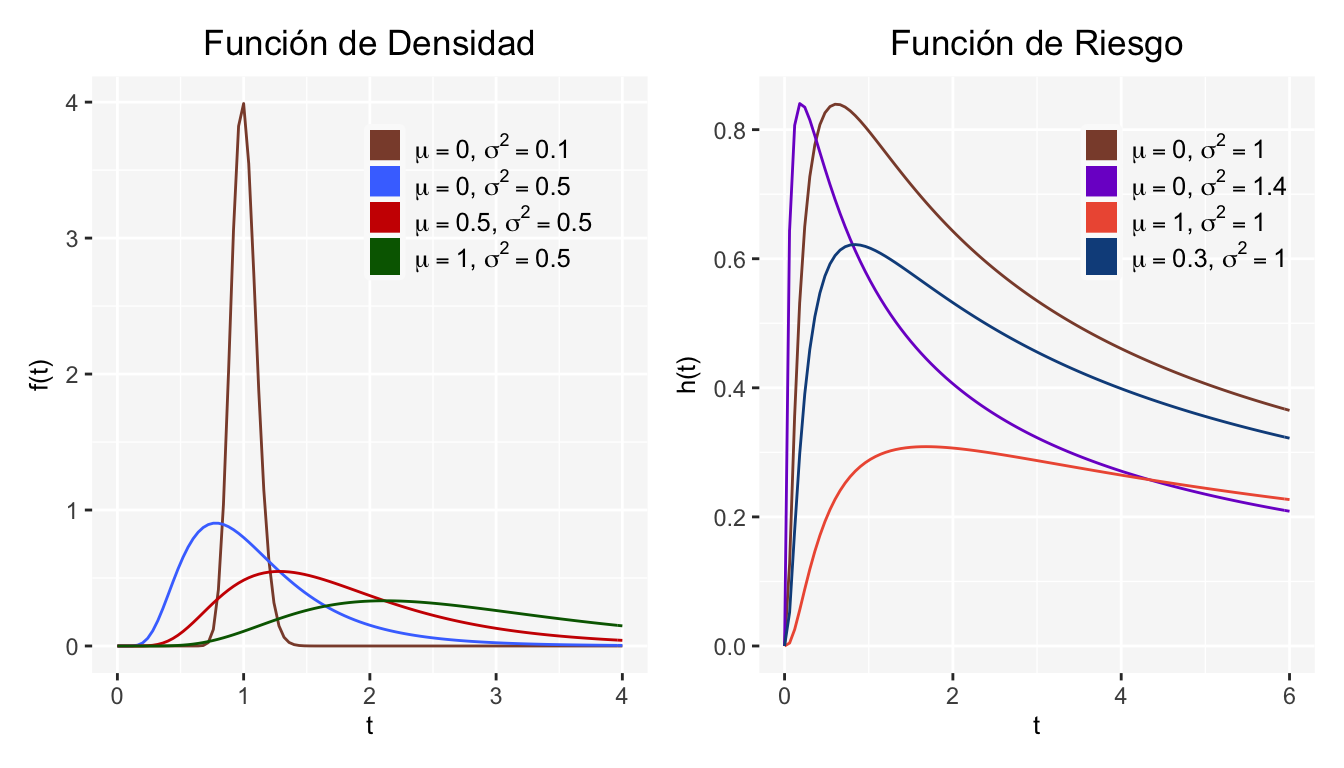
R
Para esta distribución el sufijo respectivo será *lnorm, de tal manera que se tienen las siguientes funciones mencionando la interpretación de sus resultados:
rlnorm(n, meanlog = 0, sdlog = 1): Muestra pseudo aleatoria de tamaño \(n\).dlnorm(x, meanlog = 0, sdlog = 1, log = FALSE): Valores de \(f(x)\).plnorm(q, meanlog = 0, sdlog = 1, lower.tail = TRUE, log.p = FALSE): Valores de \(F(x)\).qlnorm(p, meanlog = 0, sdlog = 1, lower.tail = TRUE, log.p = FALSE): Cuantil \(t_p\).
En este caso, es evidente que meanlog correspondería al parámetro de escala \(\mu\) y sdlog al parámetro de forma \(\sigma\). Finalmente se menciona que estos parámetros no se deben confundir explícitamente con los de una distribución normal.
Ejemplo
El tiempo de muerte en días después de un trasplante de médula sigue una distribución \(log-normal\) con \(\mu = 3.177, \sigma = 2.084\). Calcular lo siguiente
- La media y la mediano tiempo de muerte
- La probabilidad de que un individuo sobreviva 200 días después de un trasplante.
Soluciones
- Mediana: \(t_{0.5} =e^{\mu}\) cuando \(T\sim log-normal \implies\) Mediana de tiempo de muerte: \(t_{0.5} = e^{3.177} = 23.97\).
- Media: \(\mathbb{E}(T) = e^{\mu+\sigma^2/2}\) cuando \(T\sim log- normal \implies\) Media de tiempo de muerte: \(\mathbb{E}(T) = e^{3.177+\frac{(2.084)^2}{2}} = 210.29\) días.
Entonces si sobrevivieron 23.97, queda una gran cantidad de días donde, en promedio son 210.29.
- \(S(200) = 1-\Phi\left(\frac{\ln(200)-3.177}{2.084}\right) = 1-0.8438 = 0.15436\).
5.4 Modelo Log-Logístico
El modelo Log-Logístico es derivado de la distribución Logística. Se dice que \(T\) tiene distribución Log-Logística si \(Y=ln(T)\) sigue una distribución Logística con parámetros \(\mu\) y \(\sigma ^2\).
Función de Densidad
\[ f(t)=\frac{\alpha \lambda (\lambda t)^{\alpha-1}}{(1+(\lambda t)^\alpha)^2} \]
con \(\alpha=\frac{1}{\sigma}\) y \(\lambda=exp(-\frac{\mu}{\sigma})>0\). \(\alpha\) es el parámetro de forma y \(\lambda\) es el parámetro de escala.
Función de Supervivencia
\[ S(t)=\frac{1}{1+(\lambda t)^\alpha} \]
Función de Riesgo
\[ h(t)=\frac{f(t)}{S(t)}=\frac{\alpha \lambda (\lambda t)^{\alpha-1}}{1+(\lambda t)^\alpha} \]
La función de riesgo es monótona decreciente para \(\alpha \leq 1\), y para \(\alpha> 1\) la función de riesgo crece hasta alcanzar un máximo en \(t=(\frac{\alpha-1}{\lambda})^{\frac{1}{\alpha}}\) y luego decrece a cero cuando \(t \rightarrow \infty\).
Gráficas
Algunos ejemplos de las gráficas de \(f(t)\) y \(h(t)\) para la distribución Log-Logística:
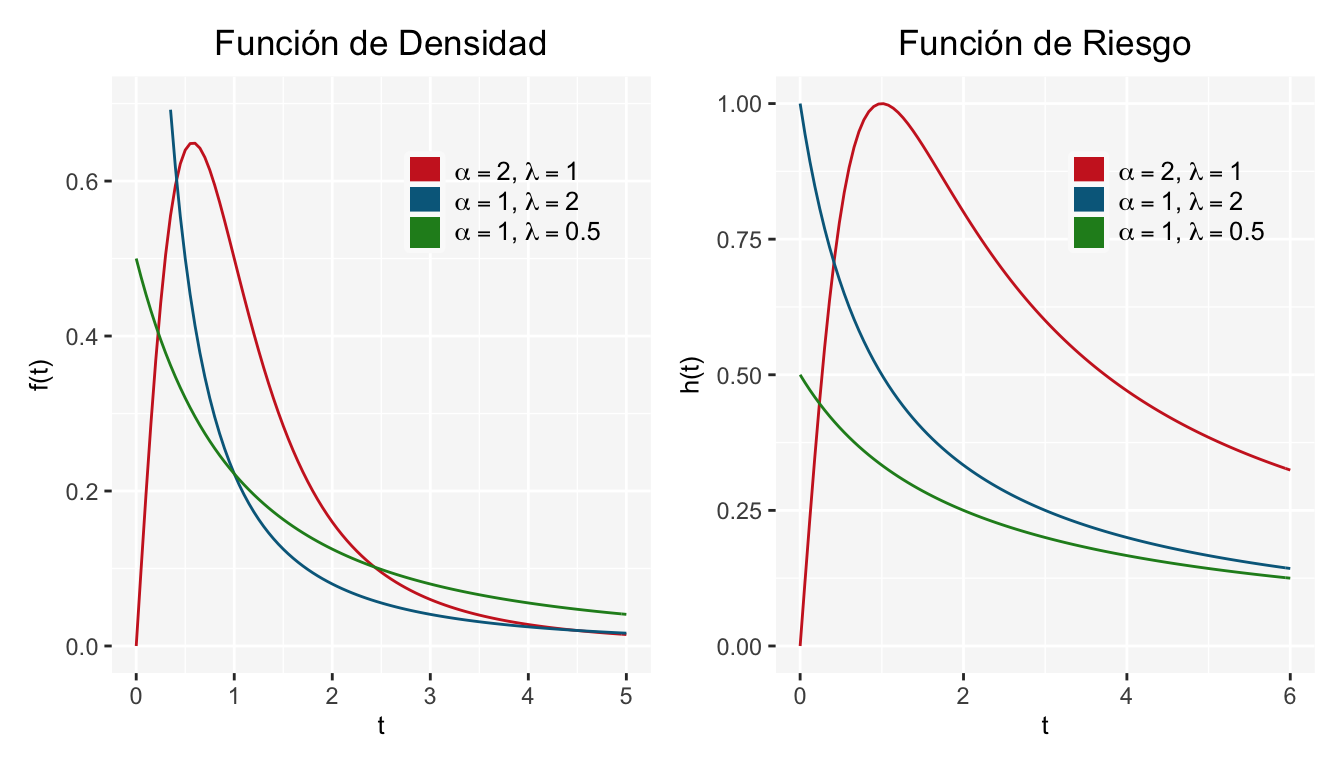
R
Para esta distribución se recomienda descargar y utilizar el paquete actuar, en la cual vienen un conjunto de funciones similares a las anteriores, de hecho el sufijo respectivo será *llogis y, de manera análoga a las anteriores funciones, se tiene lo siguiente:
rllogis(n, shape, rate = 1, scale = 1/rate): Muestra pseudo aleatoria de tamaño \(n\).dllogis(x, shape, rate = 1, scale = 1/rate, log = FALSE): Valores de \(f(x)\).pllogis(q, shape, rate = 1, scale = 1/rate, lower.tail = TRUE, log.p = FALSE): Valores de \(F(x)\).qllogis(p, shape, rate = 1, scale = 1/rate, lower.tail = TRUE, log.p = FALSE): Cuantil \(t_p\).
En este caso, como en la exponencial y la weibull, rate correspondería al parámetro \(\lambda\) y shape al parámetro de forma \(\alpha\).
5.5 Modelo Gamma
La distribución Gamma, que incluye a las distribuciones exponencial y ji-cuadrada, ha sido utilizada como un modelo para problemas de confiabilidad industrial, hepatogramas en adultos normales y en pacientes con cirrosis, en supervivencia de plaquetas, entre otros. Este modelo tiene dos parámetros: \(\beta\) es el parámetro de forma y \(\lambda\) es el parámetro que modifica de escala; estrictamente hablando \(\lambda\) es la tasa: \(\lambda =\frac{1}{s}\) donde \(s\) sería el verdadero parámetro de escala.
Función de Densidad
\(f(t)\) está dada por:
\[ f(t)=\frac{\lambda^\beta}{\Gamma(\beta)}t^{\beta-1}exp(-\lambda t); \ \ \ \lambda,\beta>0 \]
Función de Supervivencia
\[ S(t)=1-Ig(\lambda t, \beta) \]
donde6:
\[ Ig(t,\beta)=\frac{1}{\Gamma(\beta)}\int_0^{t}u^{\beta-1}e^{-u}du \] Al igual que un modelo \(Weibull(\lambda, alpha = 1)\), la distribución exponencial es un caso particular del modelo \(Gamma(\lambda,\beta = 1)\). Cuando \(\beta \rightarrow\infty\), modelo gamma se aproxima a una distribución normal.
Función de Riesgo
\[ h(t)=\frac{f(t)}{S(t)}=\frac{\frac{\lambda^\beta}{\Gamma(\beta)}t^{\beta-1}exp(-\lambda t)}{1-Ig(\lambda t, \beta)} \]
Esta función de riesgo tiene distintos comportamientos:
- Es monótona creciente para \(\beta>1\). En este caso sucede que \(h(0)=0\) y \(\underset{t\rightarrow\infty}{h(t)} \rightarrow \lambda\). Además, la moda de la distribución es \(t = \frac{\beta-1}{\lambda}\)
- Es monótona decreciente con \(\beta <1\). En tal caso \(h(0) = \infty\) y \(\underset{t\rightarrow\infty}{h(t)} \rightarrow \lambda\).
Parámetros
Si \(T\sim Gamma(\beta,\lambda)\) entonces:
\[ \begin{array}{ccc} \mathbb{E}[T]=\frac{\beta}{\lambda} & \mbox{y} & Var[T]=\frac{\beta}{\lambda^2} \end{array} \]
Las demostraciones de las igualdades de la esperanza y varianza se quedan de ejercicio al alumno.
Gráficas
Se muestran ejemplos de las gráficas de \(f(t)\) y \(h(t)\) para el modelo Gamma:
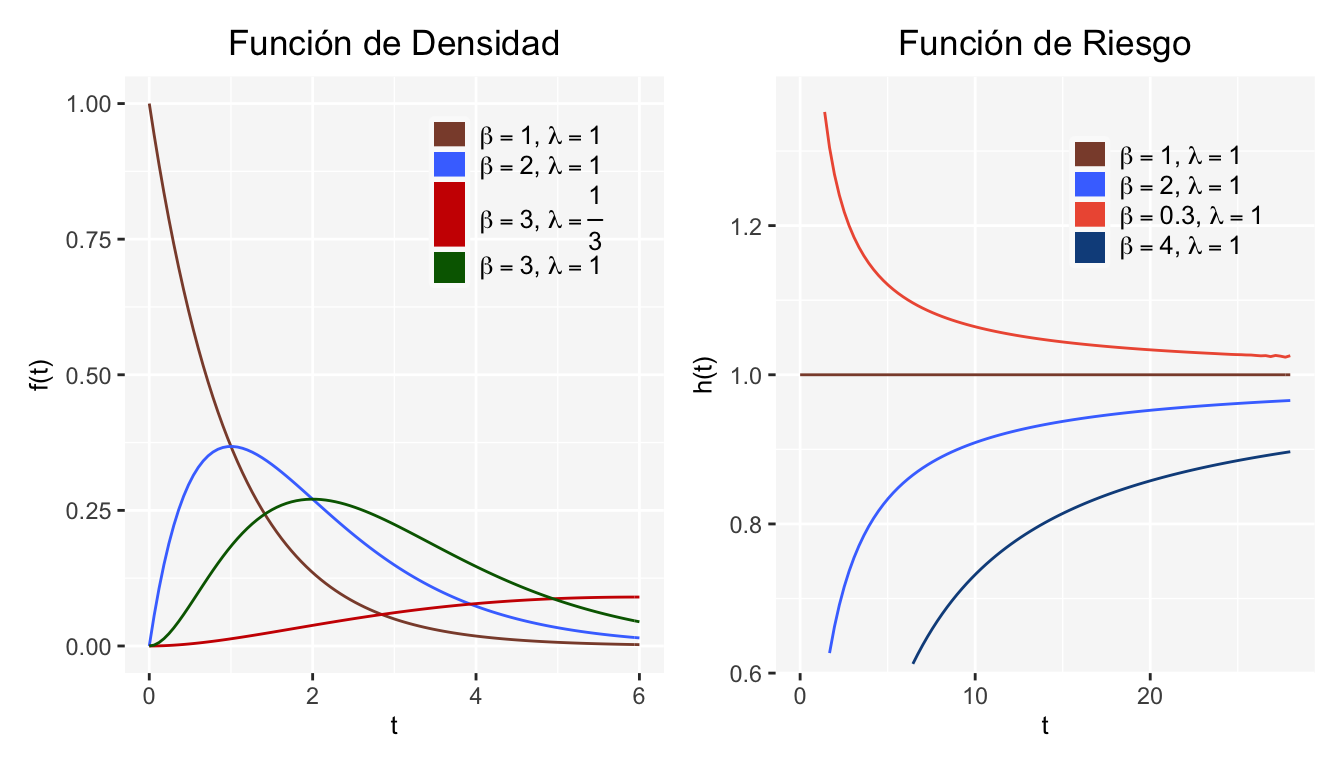
R
Para esta distribución el sufijo respectivo será *gamma, de tal manera que se tienen las siguientes funciones mencionando la interpretación de sus resultados:
rgamma(n, shape, rate = 1, scale = 1/rate): Muestra pseudo aleatoria de tamaño \(n\).dgamma(x, shape, rate = 1, scale = 1/rate, log = FALSE): Valores de \(f(x)\).pgamma(q, shape, rate = 1, scale = 1/rate, lower.tail = TRUE, log.p = FALSE): Valores de \(F(x)\).qgamma(p, shape, rate = 1, scale = 1/rate, lower.tail = TRUE, log.p = FALSE): Cuantil \(t_p\).
Como en el caso de la exponencial, se recomienda tener precaución ya que el parámetro rate es el que corresponde al parámetro \(\lambda\) en este trabajo.
5.6 Modelo Gamma Generalizada
Finalmente, se presenta el modelo Gamma Generalizada con dos parámetros de forma y un parámetro de que modifica la escala \(\alpha\), \(\beta\) y \(\lambda\) respectivamente.
Función de Densidad
\(f(t)\) está dada por:
\[ f(t)=\frac{\alpha\lambda^{\beta\alpha}}{\Gamma(\beta)}t^{\alpha\beta-1}\exp(-\lambda t)^\alpha; \ \ \ \lambda,\alpha, \beta>0 \]
Función de Supervivencia
\[ S(t)=1-Ig((\lambda t)^\alpha, \beta) \]
Esta distribución se reduce a las siguientes
- \(Exponencial\) cuando \(\beta = \alpha = 1\).
- \(Weibull\) cuando \(\beta = 1\).
- \(Gamma\) cuando \(\alpha = 1\).
- Tiende a la log-normal cuando \(\beta\rightarrow\infty\).
R
Para esta distribución se recomienda descargar y utilizar el paquete ggamma, en la cual vienen un conjunto de funciones similares a las anteriores. Aquí el respectivo sufijo será *ggamma y, de manera análoga a las anteriores funciones, se tiene lo siguiente:
rggamma(n, a, b, k): Muestra pseudo aleatoria de tamaño \(n\).dggamma(x, a, b, k, log = F): Valores de \(f(x)\).pggamma(p, a, b, k, lower.tail = TRUE, log.p = FALSE): Valores de \(F(x)\).qggamma(p, shape, rate = 1, scale = 1/rate, lower.tail = TRUE, log.p = FALSE): Cuantil \(t_p\).
Para este caso, se tiene una parametrización de uso común en distintas fuentes. a = \(\frac{1}{\lambda}\), b = \(\alpha\) y k = \(\beta\).
Ejemplo
El tiempo de vida en meses de cierta especie de ratón sigue una distribución \(gamma(\beta = 3, \lambda = 0.2)\).
- Calcular la probabilidad de que un ratón sobreviva más de 18 meses.
- ¿Cuál es la probabilidad de que un ratón muera en el primer año de vida?
- ¿Cuál es la esperanza de vida media de esta especia?
Soluciones
- \(S(18) = 1-F(18) = 1-\) 0.6972532 = 0.3027468
- \(F(12) =\) 0.4302913
- \(\mathbb{E}(T) = \frac{\beta}{\lambda} = \frac{3}{0.2} = 15\) meses.
Cabe señalar que hasta este punto no hemos introducido datos censurados a los modelos.
Un parámetro de escala modifica la escala o dispersión de la distribución ya sea que entre mayor sea este parámetro mayor dispersión se tendrá o se tenga el caso contrario como en una log-logistica. En el siguiente enlace se puede encontrar mayor información sobre esto así como animaciones para un mejor entendimiento.↩︎
Un parámetro de forma es aquel que no es de escala ni de localización o una función de estos, ya que su único propósito es modificar la forma de la distribución de manera distinta a estos anteriores, es decir que no sólo traslada o afecta la variabilidad de la misma.↩︎
Esta función se llama función gamma incompleta y en algunas fuentes se puede encontrar esta en particular como lower incomplete gamma function. Cuando se tiene \(\int_x^{\infty}u^{\beta-1}e^{-u}du = \Gamma(x, \beta)\) se le conoce como upper incomplete gamma function, la cual es una generalización de la función gamma: \(\Gamma(x, 0) = \Gamma(x)\). Originalmente esta función no tiene el cociente que se esta utilizando en este caso, esto es un efecto de normalizar la función como se puede ver en el siguiente enlace. Algunas veces esta función es conocida directamente como función gamma incompleta como en (Klein and Moeschberger 2006)↩︎