Capítulo 10 Modelo de Riesgos Proporcionales
Cuando se desea comparar 2 o más grupos de tiempos-evento, si los grupos son “similares” entonces se les pueden aplicar los métodos no paramétricos vistos. Usualmente los individuos en los grupos tienen características adicionales que pueden afectar el resultado, por ejemplo, variables como: edad, género, nivel socioeconómico, consumo del alcohol, ritmo cardiaco, nivel de colesterol, etcétera.
Dichas variables pueden usarse como covariables (variables explicativas, factores de riesgo, variables independientes) en un modelo que explique la variable respuesta. Así, después de ajustar las covariables, la comparación de tiempos de supervivencia entre grupos deberá tener menos sesgo y ser más precisa que la simple comparación de tiempos de supervivencia.
Otro problema a resolver será predecir la distribución del tiempo de ocurrencia de cierto evento a partir de un conjunto de covariables.
Los datos estarán dados de la siguiente forma: \((t_i, \delta_i,x_i)\) con \(i = 1,...n\), donde:
- \(i\): individuos.
- \(t_i\): tiempo de falla o censura.
- \(\delta_i\): indicador de falla o censura.
- \(x_i\): conjunto de covariables.
Nota:
- \(X_i =(X_{i1}, X_{i2}, ..., X_{ip})\); donde \(p\)= número de covariables.
- \(X_i\) puede depender del tiempo, es decir, \(X_{ik}\) es una v.a que cambia en el tiempo (peso, colesterol, etc.).
Sea \(h_i(t|X_i)\) la función de riesgo al tiempo \(t\) del individuo \(i\) dadas las covariables \(X_i\) (vector de riesgo). El modelo propuesto por Cox (1972) es:
\[ h_i(t) = \varphi(X_i ;\theta)\cdot h_0(t) \] Donde:
- \(\theta=(\theta_1,..., \theta_p)\) es el vector de \(p\) parámetros asociados a las covariables (coeficientes de regresión).
- \(\varphi(\cdot,\cdot)\) es la función liga de las covariables con el tiempo t.
- \(h_{0}(t)\) es la función de riesgo base.
La función \(\varphi(\cdot,\cdot)\) debe satisfacer que \(\varphi(0,\theta) =1\), esto para que, en ausencia de covariables, se tenga que \(h_i(t) = h_0(t)\).
La forma más común de \(\varphi(X_i, \theta)\) es \(\varphi(X_i, \theta) = e^{X_i^{'} \theta}\) (Supone que \(X_i\) no tiene intercepto), entonces:
\[ h_i(t) = e^{X_i^{'} \theta}\cdot h_0(t) \]
Si aplicamos logaritmo tenemos que:
\[ \ln(h_i(t)) = X_i^{'}\theta + \ln(h_0(t)) \]
\[\begin{equation} \Longrightarrow X_i^{'}\cdot\theta = ln \left({\frac{h_i(t)}{h_0(t)}}\right) \tag{10.1} \end{equation}\]
Es decir, el cociente de la función de riesgo del individuo \(i\) con respecto al riesgo base será igual a una forma lineal de las covariables.
El nombre de riesgos proporcionales se deriva del cociente de las funciones de riesgo de dos individuos:
\[ \frac{h_i(t)}{h_j(t)} = \frac{e^{X_i^{'} \theta}\cdot h_0(t)}{e^{X_j^{'} \theta} \cdot h_0(t)} = e^{(X_i-X_j)' \theta} \]
A la expresión anterior se le conoce como riesgo relativo y es constante en el tiempo, cuyo valor depende simplemente de la diferencia entre valores de las covariables de los dos individuos14.
Si \(X_{1i} = 1\) y \(X_{1j} = 0\), representan tratamiento y placebo respectivamente, y si todas las demás covariables se mantienen constantes, entonces \(e^{\theta_1}\) es el riesgo de que se presente la falla con el tratamiento relativo a que se presente la falla con el placebo.
\[\frac{h_i(t)}{h_j(t)} = e^{\theta_1}\] Bajo el modelo de riesgos proporcionales, las funciones de supervivencia y densidad del individuo \(i\) son: \[S_i(t)=\{S_0(t)\}^{exp(X_i'\theta)}\] \[f_i(t)=e^{(X_i'\theta)}h_0(t)\{S_0(t)\}^{exp(X_i'\theta)}\]
donde \(S_0(t)=exp\{-H_0(t)\}\) es la función de supervivencia base y \(H_0(t)\) la función de riesgo acumulado base. Una consecuencia del supuesto de proporcionalidad entre los riesgos de dos individuos \(i,j\) con covariables \(X_i,X_j\) es que las funciones de riesgo y supervivencia no se intersectan.
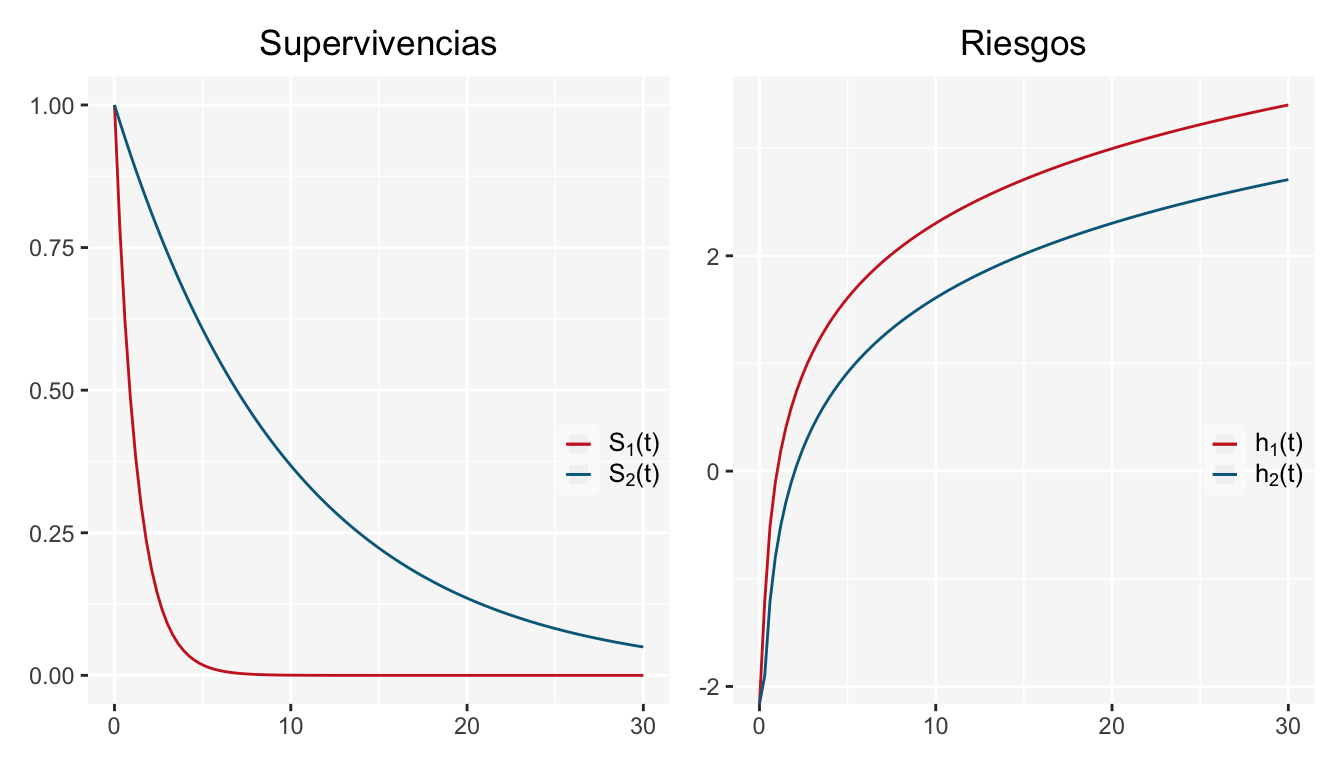
NOTA: Si \(S_0(t)\) es miembro de una familia paramétrica, por lo general, \(S_i(t)\) no es miembro de la misma familia. Véase los siguientes ejemplos
Riesgo base Weibull: \(h_0(t) = \lambda\alpha t^{\alpha-1}\) \[ \begin{array}{cc} \implies h_i(t) = \lambda \alpha t^{\alpha-1}e^{X_i^{'}\theta} = \lambda e^{X_i^{'}\theta}\alpha t^{\alpha-1}&\therefore h_i\sim Weibull(\alpha, \lambda e^{X_i^{'}\theta}) \end{array} \]
Riesgo base log-logistico: \(h_0(t) = \frac{\alpha \lambda t^{\alpha-1}}{(1+\lambda t^{\alpha})}\) \[ \implies h_i(t) = \frac{e^{Xi^{'}\theta}\alpha t^{\alpha -1}}{(1+\lambda t^{\alpha})} \]
Riesgo base Gamma: \(S_0(t) = 1-lg(\lambda t, \beta)\) \[ S_i(t) = \{S_0(t)\}^{e^{X_i^{'}\theta}} = \left(1-lg(\lambda t, \beta)\right)^{e^{X_i^{'}\theta}} \]
10.1 Inferencia sobre \(\theta\)
La inferencia para los modelos de riesgos proporcionales paramétricos se hacen por máxima verosimiliutd.
Sea \((t_i, \delta_i, X_i)\)
- i : individuos.
- \(t_i\): tiempo de fallo o censura.
- \(\delta_i\): Indicador de fallo o censura.
- \(X_i\): Covariables.
Sean \(h_0(t|\alpha, \lambda)\) y \(S_0(t|\alpha, \lambda)\) funciones de riesgo y supervivencia base.
Entonces la función de verosimilitud para \((\theta, \alpha, \lambda)\) será:
\[ \begin{split} \mathscr{L}(\theta, \alpha, \lambda) & =\prod_{i = 1}^{n}\{f_i(t)\}^{\delta_{i}}\{S_i(t)\}^{1-\delta_{i}}\\ & =\prod_{i = 1}^{n}\left\{e^{X_i^{'}\theta}h_0(t)S_0(t)^{e^{X_i^{'}\theta}}\right\}^{\delta_{i}}\left\{S_0(t)^{e^{X_i^{'}\theta}}\right\}^{1-\delta_i}\\ & =\prod_{i = 1}^{n}\left\{e^{X_i^{'}\theta}h_0(t)\}^{\delta_{i}}\{S_0(t)^{e^{X_i^{'}\theta}}\right\} \end{split} \]
- Los estimadores máximo verosímil se obtienen numéricamente.
- La forma explicita de \(\mathscr{L}(\theta, \alpha, \lambda)\) dependerá de la elección de \(h_0\).
- Inferencia para los parámetros más allá de la estimación puntual se basa en los resultados asintóticos.
10.2 Estimación Semiparamétrica (Verosimilitud parcial).
El modelo de riesgos proporcionales semiparamétrico surge cuando la función de riesgo base \(h_0(t)\) se considera como una parámetro desconocido, y en este caso es necesario hacer inferencia para \(\theta\) y \(h_0(t)\). El parámetro de interés más importante del modelo es \(\theta\) y entonces \(h_0(t)\) es considerado un parámetro de ruido.
Supongamos que los datos consisten en el vector de observaciones \(T = (T_1, ..., T_n)\) de la densidad \(f(t|\theta,\eta)\) donde \(\theta\) es el vector de parámetros de interés y \(\eta\) es parámetro de ruido.
Sean \(t_{(1)}<t_{(2)}<...<t_{(D)}\) los tiempos de fallo observados de manera exacta.
Sea \(X_{(j)}\) la variable asociada al individuo con tiempo de fallo \(t_{(j)}\).
Definimos \(R(t_{(j)})\) como el conjunto de todos los individuos en riesgo justo antes de \(t_{(j)}\).
Entonces la verosimilitud parcial para \(\theta\) es
\[ _p\mathscr{L}(\theta) = \prod_{j = 1}^{D}\frac{h_{j}(t_{(j)})}{\sum\limits_{i\in R(t_{(j)})}h_{i}(t_{(j)})} = \prod_{j = 1}^{D}\frac{\exp\left(X_{(j)}^{'}\theta\right)}{\sum\limits_{i\in R(t_{(j)})}\exp\left(X_{i}^{'}\theta\right)} \]
OBS :
- \(_p\mathscr{L}(\theta)\) no depende de \(h_0(t)\)
- El numerador depende sólo de la información del individuo que falla.
- El denominador usa información de todos los individuos que aún no han experimentado fallo incluyendo censurados.
- La verosimilitud parcial se trata como cualquier función de verosimilitud (aplica logaritmo, derivada igual a cero,…)
- \(\theta\) es un vector de dimensión \(p\implies\) se obtendrán \(p\) derivadas parciales. La mayoría de los paquetes usan algoritmos de Newton-Raphson para resolver el sistema de ecuaciones simultaneas.
- Pruebas de hipótesis e intervalos de confianza para \(\theta\) se pueden obtener con distribución asintótica normal con media \(\theta\) y matriz de varianzas y covarianzas.
10.3 Estimador de Breslow (\(H_{0}(t)\) y \(S_{0}(t)\))
Si la funciones base son también de interés, se puede utilizar el estimador propuesto por Berslow (1974) que es una generalización del estimador de Nelson-Aalen.
\[\hat{H_{0}}(t) = \sum_{i:t_i\leq t}\left \{\frac{\delta_i}{\sum_{j = 1}^nY_j(t_i)e^{X_j^{'}\hat{\theta}}} \right \} = \frac{\mbox{Fallecidos}}{\mbox{Individuos en riesgo}}\] donde \(Y_i(t) = \mathbb{1}_{\{t_i\geq t\}}\) indicadora si \(\hat{\theta} = 0\) y \(\hat{H_0}(t)\) es el estimador de Nelson-Aalen visto previamente.
\[\therefore \hat{S_0(t)} = exp\{-\hat{H_0}(t)\} = e^{\sum_{i:t_i\leq t}\left \{\frac{\delta_i}{\sum_{j = 1}^nY_j(t_i)e^{X_j^{'}\hat{\theta}}} \right \}}\]
Notas
- En el caso de que se presenten empates (múltiples individuos con el mismo tiempo de fallo) la \(_p\mathscr{L}(\theta)\) debe ajustarse para que se considere la naturaleza discreta de las observaciones.
- El modelo de riesgos proporcionales permite la incorporación de covariables dependientes en el tiempo.
Ejemplo 1
Un estudio sobre la supervivencia clasifica según la raza en: blanco, negro e hispano. Entonces las variable \(X_1\) toma los siguientes valores:
\[ \begin{array}{ll} X_1 = \mbox{1 si es blanco } \\ X_1 = \mbox{2 si es negro } \\ X_1 = \mbox{3 si es hispano} \\ \end{array} \]
Sin embrago, también podría plantearse como dos variables \(X_1\) y \(X_2\) \[ \begin{array}{ll} X_1 = 1 \mbox{ si es blanco, 0 en otro caso.}\\ X_2 = 1 \mbox{ si es negro, 0 en otro caso}\\ \end{array} \]
Entonces, el modelo de riesgos proporcionales será: \(h(t|X) = h_0e^{\beta_1X_1+\beta_2X_2}\)
- Si \(h(t|X_1=1, X_2 = 0) = h_0(t)e^{\beta_1}\longrightarrow\) Riesgo de blanco
- Si \(h(t|X_1=0, X_2 = 1) = h_0(t)e^{\beta_2}\longrightarrow\) Riesgo de negro
- Si \(h(t|X_1=0, X_2 = 0) = h_0(t)\longrightarrow\) Riesgo de hispano (riesgo base)
Riesgos relativos:
- Entre negro e hispano: \(\frac{h(t|X_1 = 0, X_2 = 1)}{h(t|X_1 = 0, X_2 = 0)} = \frac{h_0(t)e^{\beta_2}}{h_{0}(t)}=e^{\beta_2}\)
Es decir, \(e^{\beta_2}\) son las veces que el riesgo que tienen los negros en comparación con los hispanos.
- Se busca que el riesgo relativo sea \(\neq1\) para poder decir que la categoría segmenta datos.
Ejemplo 2
Un estudio con 863 pacientes con trasplante de hígado. Dos de las variable que se recabaron de los pacientes fueron, género y raza. Entonces los pacientes en el estudio se dividieron en las siguientes categorías
\[ \begin{array}{ll} 432 \mbox{ hombres blancos}\\ 92 \mbox{ hombres negros}\\ 286 \mbox{ mujeres blancas}\\ 59 \mbox{ mujeres negras}\\ \end{array} \]
Para ajustar un modelo de riesgos proporcionales a estos datos, una opción es definir 3 covariables:
\[ \begin{array}{ll} Z_1 = 1 \mbox{ hombre negro, 0.e.o.c}\\ Z_2 = 1 \mbox{ hombre blanco, 0.e.o.c}\\ Z_3 = 1 \mbox{ mujer negra, 0.e.o.c}\\ \end{array} \] Y el modelo para la función de riesgo será: \[h(t|Z) = h_0(t)exp \{ \theta_1Z_1 + \theta_2Z_2 + \theta_3Z_3\}\]
Los estimadores máximo verosímil son \(\hat{\theta_1} = 0.160\), \(\hat{\theta_2} = 0.298\), \(\hat{\theta_3} = 0.657\).
Riesgo relativo de hombre negro con mujer blanca :
\[h(t|Z) = \frac{h_0(t)exp\{0.160\}}{h_0(t)exp\{0\}} = e^{0.160} = 1.17\] \(\therefore\) Los hombres negros son más propensos a morir por trasplante de hígado que las mujeres blancas; es decir, por cada mujer blanca, un hombre negro (1.17) muere en el trasplante.
En el caso de un hombre negro y un hombre blanco
\[h(t|Z) = \frac{h_0(t)exp\{0.160\}}{h_0(t)exp\{0.298\}} = e^{-0.088} = 0.9157609\]
Otra opción de plantear el modelo es con 2 covariables y una interacción, y quedaría de la siguiente forma:
\[ \begin{array}{ll} Z_1 = 1 \mbox{ Si es mujer, 0 e.o.c}\\ Z_2 = 1 \mbox{ Si es negro(a), 0 e.o.c}\\ Z_3 = Z_1\cdot Z_2 \mbox{ Esta variable tomará el valor 1 si es mujer negra, y 0 e.o.c} \end{array} \]
Y el modelo para la función de riesgo será: \(h(t|Z) = h_0exp\{\theta_1Z_1+\theta_2Z_2+\theta_3Z_1Z_2\}\).
Los estimadores máximo verosímil son \(\hat{\theta_1} = -.2484, \hat{\theta_2} =-.0888, \hat{\theta_3} = .7435\). Hay que notar que la interpretación de las \(\theta's\) será diferente y en este caso el parámetro de interés será el de la interacción (\(\theta_3\))
Riesgos relativos :
\[\frac{\mbox{Hombre negro}}{\mbox{Mujer blanca}} = \frac{h_0(t)exp\{-0.0888\}}{h_0exp\{-0.2484\}} = e^{-(0.0888+0.2484)} = e^{-.1596} = 1.17\]
Véase que es el mismo resultado que se obtuvo en el modelo anterior, por lo que se sigue conservando el mismo riesgo independiente del modelo.
Ejercicios
Calcular el riesgo mujer negra relativo a mujer blanca.
Calcular el riesgo mujer negra relativo a hombre negro
Calcular el riesgo hombre blanco relativo a mujer blanca.
RECORDATORIO: Codificación de variables categóricas.
Una variable categórica con k clases se transforma en \(k-1\) variables binarias.
Ejemplo 1
X: Color de cabello {negro, cafe, rojo, blanco}. Tenemos una variable con 4 categorías. Por lo que la transformaremos en 3 variables binarias
\[ \begin{array}{l} X_1 = \mbox{1 si es negro, 0 e.o.c } \\ X_2 = \mbox{1 si es café. 0 e.o.c } \\ X_3 = \mbox{1 si es rojo, 0.e.o.c} \\ \end{array} \]
Con estas tres variables se cubren todas las opciones de color de cabello.
10.4 Significancia de los parámetros (Prueba de Wald)
¿Son significativos \(\hat{\theta_1}, \hat{\theta_2}, \hat{\theta_3}\) en ejemplo numero 2?
Similar al caso de regresión lineal, la significancia de los parámetros radica en la importancia del riesgo proporcionado por las covariables asociadas a parámetros. Y en caso de no ser significativos los parámetros, las covariables se podrían eliminar del modelo.
Prueba de hipótesis: Nos interesa hacer pruebas sobre \(\theta\), de manera general:
\[H_0:\theta_1 = \theta_{H_0}\mbox{ vs }H_1:\theta_1\neq \theta_{H_0}\] donde \(\theta = (\theta_1^t, \theta_2^t) = (\theta_1, \theta_2, ..., \theta_p)\)
- \(\theta_1:\) Es el vector de \(q*1\) (\(q\) parámetros de interés)
- \(\theta_2:\) Los parámetros restantes (\(p-q\))
Partimos la matriz de información : \(I = \begin{pmatrix}I_{11} & I_{12} \\ I_{21} & I_{22}\end{pmatrix}\)
Donde \(I_{11}\), \(I_{22}\) segundas derivadas de la función de verosimilitud.
La Prueba de Wald se define como:
\[ X_w^2 =(\hat{\theta_1}-\hat{\theta_{H_0}})^{'}[I^{*}(\theta)]^{-1}(\hat{\theta_1}-\hat{\theta_{H_0}}) \]
Donde \(I^{*}(\theta)\) es la matriz \(q*q\) superior de \(I\).
Para muestras grandes, la estadística de prueba: \(X_w^2\sim\chi_{(q)}^2\)
Un criterio de información es el proporcionado por el criterio de Aikaike (\(ACI\)):
\[AIC = -2log{\mathscr{L}}+kp\]
- \(\mathscr{L}\): Función de verosimilitud.
- \(k\): Cte.(usualmente igual a 2).
- \(p\): # de parámetros en el modelo.
Para la construcción del modelo usando el modelo de riesgos proporcionales de Cox, se puede usar el estadístico de Wald para seleccionar covariables significativas15 y considerando el valor del AIC para evaluar la mejora en el modelo16.
10.5 Estimación de \(S(t)\) después de obtener las estimaciones de los parámetros del modelo de Cox
Hasta el momento se han dado estimadores para \(\theta\) y pruebas sobre dicho parámetro; es decir, teniendo el modelo de riesgos proporcionales \(h(t|X) = h_0(t)e^{X^{'}\theta}\) y ajustando dicho modelo a nuestros datos obtenemos \(\hat{\theta}\). Ahora lo que se desea es la función de supervivencia con el conjunto de covariables \(X_i\).Para ello sea \(t_1<t_2, \dots<t_D\) todos los tiempos de falla y \(d_i\) el número de fallas del tiempo \(t_i\). Entonces
\[ \omega(t_i, \hat{\theta}) = \sum_{j\in R(t_i)}\exp\left\{\sum_{h=1}^D\hat{\theta}_hX_{jh}\right\} \]
Y el estimador de la función de riesgo acumulado base será la siguiente, la cual es una función escalonada a cada tiempo de falla.
\[ \hat{H_0}(t) = \sum_{t_i\leq t}\frac{d_i}{w(t_i, \hat{\theta})} \]
Por lo que un estimador de la función de supervivencia base será el siguiente, el cual corresponde a los individuos cuyas covariables \(X\) son ceros.
\[ \hat{S}_0(t) = \exp\{-\hat{H}_0(t)\} \]
Para estimar la función de supervivencia para un individuo con covariables \(X^{*}\) se utilizará el siguiente estimador
\[ \hat{S}(t|X^{*})=\hat{S}_0(t)\exp\left\{\hat{\theta^{'}}X^{*}\right\} \] La siguiente gráfica es un ejemplo comparativo de dos estimaciones de funciones de supervivencia, una con el método de Kaplan-Meier y Cox.
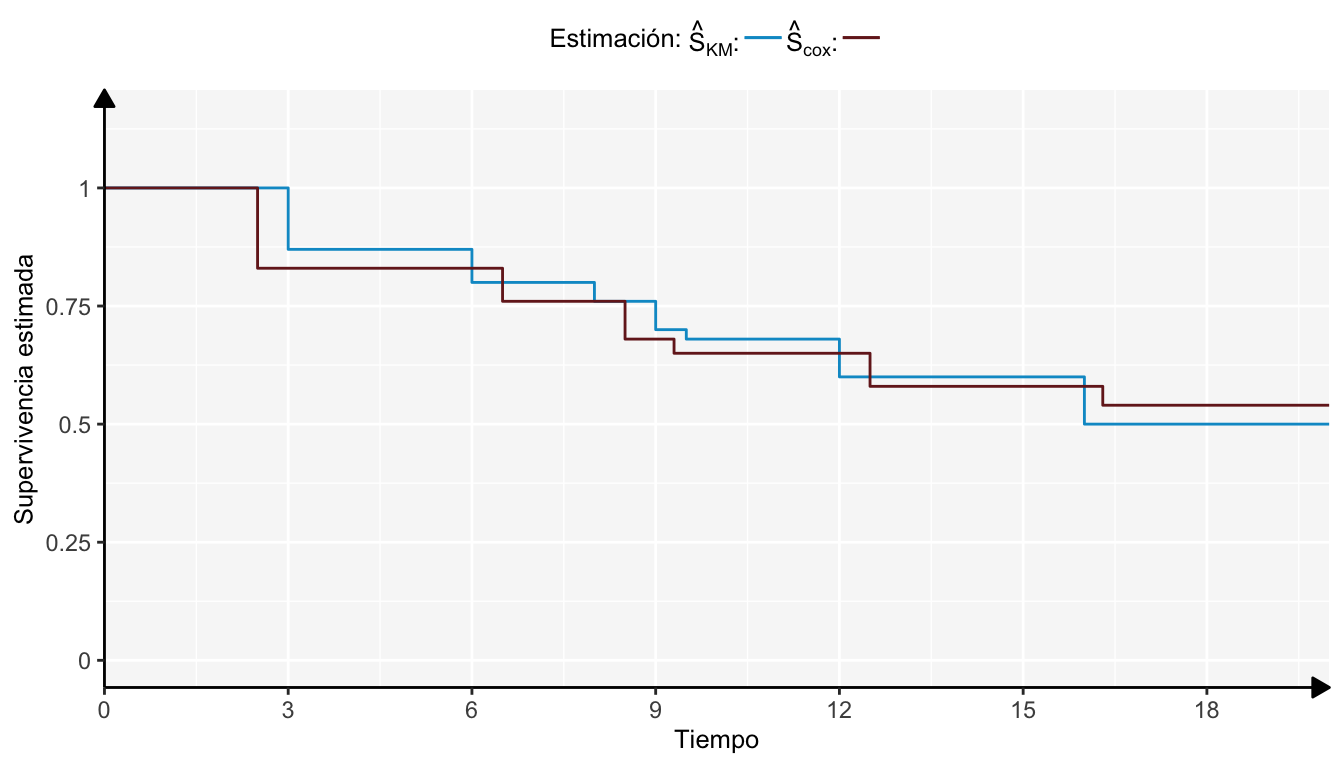
10.6 Verificación de ajuste de Modelo
Mediante gráficos de las funciones de supervivencia buscamos las funciones de supervivencia para los distintos valores de \(X\)’s donde no se crucen17.
En caso de que el modelo de Cox no cumpla con el supuesto de proporcionalidad se puede corregir el modelo mediante:
Agregar más covariables
Considerar interacciones entre las covariables
Introducir términos no lineales
Permitir que las covariables dependan del tiempo
10.7 Extensión del modelo de Cox a covariables dependientes del tiempo
Sea \(X(t)=[X_1(t),...,X_p(t)]\) es el conjunto de covariables o factores de riesgo al tiempo \(t\) que podrían afectar la distribución de la variable de supervivencia.
Entonces \(X_k(t)\)´s son covariables dependientes del tiempo cuyos valores cambian o permanecen constantes (como el caso anterior). Supondremos que los valores de estas covariables son predecibles (el valor es conocido).
Ejemplos de este tipo de variables son presión arterial, colesterol, tamaño del tumor, etc.
Sustituyendo en el modelo de Cox tenemos:
\[ \begin{split} h(t|X(t))=&h_0 (t)\cdot exp\{\beta^`\cdot Z(t )\}\\ =&h_0(t) \cdot exp \left\{ \sum_{k=1}^{p} \beta_k \cdot Z(t) \right\} \end{split} \]
Entonces para probar el supuesto de riesgos proporcionales se crea una variable artificial:
\[ X_2(t)= X_1 \cdot g(t) \]
donde \(X_1\) es una variable fija en el tiempo \(g(t)\) es una función que depende del tiempo usualmente
\[ g(t)= ln (t ) \] y se ajusta un modelo de Cox para las covariables \(X_1\) y \(X_2(t)\), tenemos
\[ \begin{split} h(t|X(t)) &= h_0 \cdot exp \{ \beta_1 X_1 +\beta_2X_2(t) \}\\ &=h_0(t) \cdot exp \{ \beta_1 X_1+\beta_2 X_1\cdot g(t) \} \end{split} \] y se realiza la prueba de hipótesis para \(\beta_2=0\). Si se desea evaluar riesgos proporcionales para 2 individuos con diferentes valores de \(X_1\)
\[ \frac{h(t|X_1)}{h(t|X_1^*)}= exp \{ \beta_1 (X_1-X_1^*)+\beta_2\cdot g(t)(X_1-X_1^*) \} \]
la cuál dependerá del tiempo si \(\beta_2 \ne 0\).
Collett, David. 2015. Modelling Survival Data in Medical Research. CRC press.
Hall, Wendy J, and Jon A Wellner. 1980. “Confidence Bands for a Survival Curve from Censored Data.” Biometrika 67 (1): 133–43.
Klein, John P, and Melvin L Moeschberger. 2006. Survival Analysis: Techniques for Censored and Truncated Data. Second. Springer Science & Business Media.
Nair, Vijayan N. 1984. “Confidence Bands for Survival Functions with Censored Data: A Comparative Study.” Technometrics 26 (3): 265–75.
No hay dependencia con el tiempo.↩︎
Recordar que por la ecuación (10.1), el modelo esta asumiendo una forma lineal de las covariables.↩︎
Para un mayor número de variables el \(AIC\uparrow\) pero para variables más significativas \(AIC\downarrow\).↩︎
Por el hecho de que se busca proporcionalidad y, por lo tanto, que la segregación separe completamente a la población.↩︎